Why Data Structures Matter

Our experience on Day 0 of JPR11 yielded a nice example of the need to choose an appropriate implementation of an abstract concept. As I mentioned in the previous post, we experimented with Michael Barker’s Scala implementation of Guy Steele’s parallelizable word-splitting algorithm (slides 51-67). Here’s the core of the issue.

Given a type-compatible associative operator and sequence of values, we can fold the operator over the sequence to obtain a single accumulated value. For example, because addition of integers is associative, addition can be folded over the sequence:

1, 2, 3, 4, 5, 6, 7, 8

from the left:

((((((1 + 2) + 3) + 4) + 5) + 6) + 7) + 8

or the right:

1 + (2 + (3 + (4 + (5 + (6 + (7 + 8))))))

or from the middle outward, by recursive/parallel splitting:

((1 + 2) + (3 + 4)) + ((5 + 6) + (7 + 8))

A 2-D view shows even more clearly the opportunity to evaluate sub-expressions in parallel. Assuming that addition is a constant-time operation, the left fold:

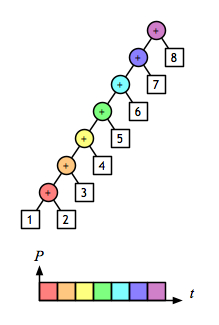
and the right fold:

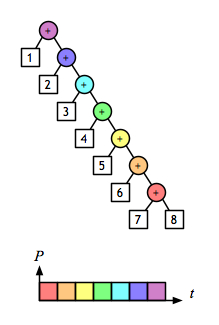
require linear time, but the balanced tree:

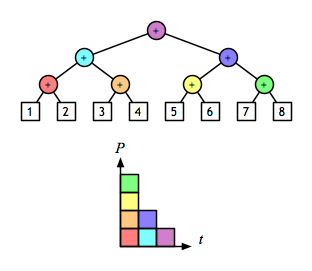
can be done in logarithmic time.

But the associative operation for the word-splitting task involves accumulating lists of words. With a naive implementation of linked lists, appending is not a constant-time operation; it is linear on the length of the left operand. So for this operation the right fold is linear on the size of the task:

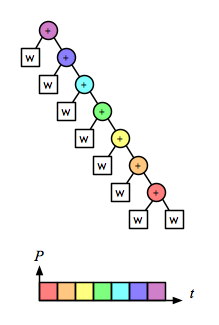
the left fold is quadratic:

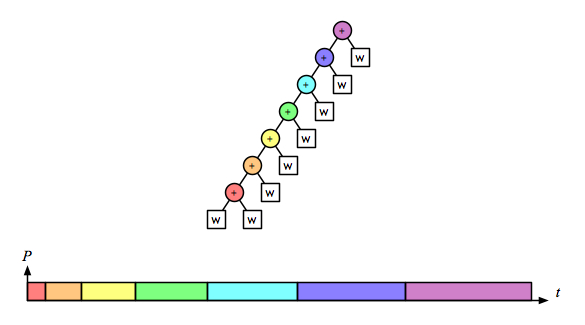
and the recursive/parallel version is linear:

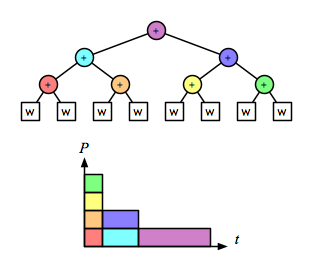
Comparing just the “parallel-activity-versus-time” parts of those diagrams makes it clear that right fold is as fast as the parallel version, and also does less total work:

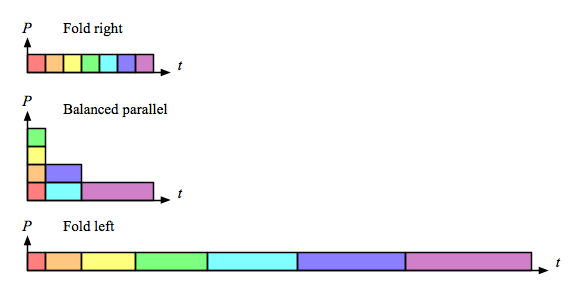
Of course, there are other ways to implement the sequence-of-words concept, and that is the whole point. This little example provides a nice illustration of how parallel execution of the wrong implementation is not a win.

---

The title of this post is a not-very-subtle (but respectful) reference to “Why Functional Programming Matters“, an excellent summary by John Hughes that deserves to be more widely read.

Purely Functional Data Structures, by Chris Okasaki, covers a nice collection of algorithms that avoid the trap mentioned above.

Also, video from this year’s Northeast Scala Symposium is now on-line for the session on functional data structures in Scala, presented by Daniel Spiewak.

Why lists are not primitive

Yesterday’s SICP study group call indulged briefly in the “why LISP hasn’t caught on” theme. I suggested that some programmers seem to have a limited tolerance for abstraction, and cited the well-known Primitive Obsession anti-pattern as evidence. One of the other participants (I’m sorry that I don’t know all the voices yet) challenged that statement. After pointing out how often the humble list is used as a universal data structure, he asked whether that was Primitive Obsession in another disguise. The conversation moved on, but that question stuck in the back of my mind.

This morning it re-emerged, dragging the following conjecture.

Although the list is a fundamental structuring mechanism in LISP, it is far from “primitive” in way that e.g. int is a primitive data type in Java. Although number theory is a well-respected branch of Mathematics, Ben Bitdiddler and Eva Lu Ator can write application code littered with int variables without ever appealing to the theoretical properties of integers–Peano’s Postulates and the like. After all, they’ve known how to count and do arithmetic since elementary school, right?

On the other hand, the LISP list is a fairly abstract and conceptual beast; list-based code normally uses recursion, either explicitly or hidden beneath the thinnest of veneers, such as map and reduce. And from there, it’s the tiniest of steps to begin reasoning about one’s code via full-blown Mathematical Induction. Furthermore, all of the conceptual properties of lists are lying there in plain sight every time a list appears. Therefore I’m encouraged to think of generalities that can re-use those tasty properties with great freedom.

In contrast, how many Java programmers routinely make the jump from

String personName;

to

public class PersonName {
    public final String firstName;
    public final String lastName;
    ...
}

to including (correctly-working!) methods for comparison and equality? (And I’m not just picking on Java; the same is true of many other “C-like” language communities.) Even though strings are comparable, and ordered composites of comparable types have an obvious default comparability, realizing that obvious comparison is tedious and error-prone. If my language trains me to think that certain things are too much trouble, then I’ll tend to stop thinking about them. And when offered a language that makes them freely available again, it will be all too easy to ask, “Who needs all that stuff?”